BIENVENIDOS
buenas, buenas, buenas, en esta paginas encontraras todo lo que necesitas para este gran problema que tienes con la cónicas lo que son parábola,elipse,hipérbola, todo este conocimiento es de décimo grado NO es avanzado ,también encontraras el conocimiento de GeoGebra de como utilizar esta herramienta y un vídeo explicativo .
COMO USAR GEOGEBRA
SECCIONES CÓNICAS
Las secciones cónicas son las curvas que obtenemos al hacer cortes rectos en un cono.

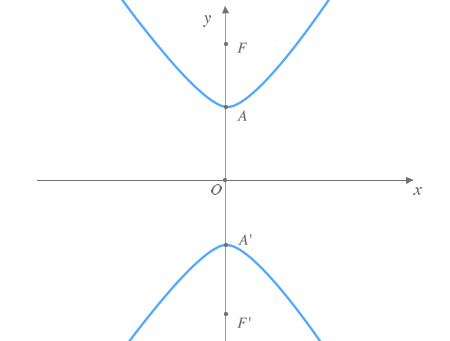
PARÁBOLA
Es el conjunto de puntos en el plano que son equis distantes con un punto fijo llamado foco y una recta fija llamada directriz; la parábola también tiene un vértice que se encuentra a la mitad entre el foco y la directriz y un eje simétrico que corre por el foco y es perpendicular a la directriz.

grafica de la elipse

DESARROLLO:
y²=20²-25²/40²

Ecuación para la parábola: x^2=4py
Una parábola tiene las siguientes propiedades:
Vértice: V (0,0)
Foco: F (0,P)
Directriz: y = -P
La parábola abre hacia arriba si P>0 o hacia abajo si P<0
-ahora unos ejercicios de parábola:
-ahora unos ejercicios de parábola:
EJERCICIOS:
1.- Reflector parabólico. En la figura se muestra una lampara con un reflector parabólico. La bombilla eléctrica esta colocada en el foco y el diámetro focal es 12cm. A) encuentre una ecuación de la parábola, B) Encuentre el diámetro de (C, D) de la abertura, 20cm del vértice.
DESARROLLO
A) F=(p,0)=(3, 0)
y^2=4px 4p=12
y^2=4(3)x p=12/4
y^2=12x p=3
B)
y^2=12x
y^2=12(20) D=8√15
y=√240 D=30,98
y=4√15
y=15,49
2.- En un puente colgante la forma de los cables de suspensión es paranoica. El puente que se muestra en la figura tiene dos torres que están a 600m una de la otra y el punto mas bajo de los cables de suspensión esta a 150m debajo de la cúspide de las torres. encuentre la ecuación de la parte parabólica de los cables, colocando el origen del sistema de coordenadas en el vértice. |Nota: Esta Ecuación se emplea para hallar la longitud del cable necesario en la construcción del puente.
DESARROLLO
x^2=4py |4p|=600m
x^2=4(150)y p=150m
x^2=600y
F=(0,p)=(0, 150)
3.- El telescopio Hale del observatorio de monte palomar tiene un espejo de 200 pulgadas, como se ve en la figura. el espejo esta construido en forma parabólica que recolecta luz de las estrellas y la enfoca en el foco primo, es decir el foco de la parábola. El espejo mide 3.79 pulgadas de profundidad en su centro. Encuentre la longitud focal de este espejo parabólico, es decir, la distancia del vértice al foco.
DESARROLLO
x^2=4py
100^2=4p(3,79)
100^2/3,79*4=p
p= 659,63 F=(0,p)=(0, 659,63)
4.- Un reflector para disco satélite es parabólico en sección transversal, con receptor en el foco F. El reflector mide 1 pie de profundidad y 20 pies de ancho de borde a borde (vea la figura). ¿A que distancia esta el receptor del vértice del reflector parabólico?
DESARROLLO
x^2=4py
10^2=4p(1)
10^2/4=p
p=25 F=(0,p)=(0, 25)
bueno si no entendiste te dejo un vídeo aquí >-< 👇👇
https://www.youtube.com/watch?v=TkRX7bwiaNU
A) F=(p,0)=(3, 0)
y^2=4px 4p=12
y^2=4(3)x p=12/4
y^2=12x p=3
B)
y^2=12x
y^2=12(20) D=8√15
y=√240 D=30,98
y=4√15
y=15,49
2.- En un puente colgante la forma de los cables de suspensión es paranoica. El puente que se muestra en la figura tiene dos torres que están a 600m una de la otra y el punto mas bajo de los cables de suspensión esta a 150m debajo de la cúspide de las torres. encuentre la ecuación de la parte parabólica de los cables, colocando el origen del sistema de coordenadas en el vértice. |Nota: Esta Ecuación se emplea para hallar la longitud del cable necesario en la construcción del puente.
DESARROLLO
x^2=4py |4p|=600m
x^2=4(150)y p=150m
x^2=600y
F=(0,p)=(0, 150)
3.- El telescopio Hale del observatorio de monte palomar tiene un espejo de 200 pulgadas, como se ve en la figura. el espejo esta construido en forma parabólica que recolecta luz de las estrellas y la enfoca en el foco primo, es decir el foco de la parábola. El espejo mide 3.79 pulgadas de profundidad en su centro. Encuentre la longitud focal de este espejo parabólico, es decir, la distancia del vértice al foco.
DESARROLLO
x^2=4py
100^2=4p(3,79)
100^2/3,79*4=p
p= 659,63 F=(0,p)=(0, 659,63)
4.- Un reflector para disco satélite es parabólico en sección transversal, con receptor en el foco F. El reflector mide 1 pie de profundidad y 20 pies de ancho de borde a borde (vea la figura). ¿A que distancia esta el receptor del vértice del reflector parabólico?
DESARROLLO
x^2=4py
10^2=4p(1)
10^2/4=p
p=25 F=(0,p)=(0, 25)
bueno si no entendiste te dejo un vídeo aquí >-< 👇👇
https://www.youtube.com/watch?v=TkRX7bwiaNU
ELIPSE
Una elipse es un conjunto de todos los puntos del plano cuya suma de desde dos puntos fijos es una constante.
aquí se va entender la elipse como un huevo o un balón de fútbol americano entiendes así que imagínate el huevo o una galaxia la elipse tiene un montón de ejemplos velos como tu quieras, si mas preámbulos empecemos:
aquí se va entender la elipse como un huevo o un balón de fútbol americano entiendes así que imagínate el huevo o una galaxia la elipse tiene un montón de ejemplos velos como tu quieras, si mas preámbulos empecemos:
grafica de la elipse

Ecuación para la elipse :
1 . 2.
1 . 2.
a>b>0 a>b>0
- tienes que tener cuidado con el (a) y el (b) cumpliendo lo que dice arriba, si no la ecuación sale mal, si es horizontal o vertical el huevo (elipse) explico, si la (a) esta arriba de la x el huevo es horizontal pero si esta en la (b) el huevo es vertical.
Una elipse tiene las siguientes si vas a graficar tienes que tener esto pendiente:
como en la parábola tiene foco la elipse tiene dos focos y de esta manera se hallan
si tienes el punto (C) tienes los focos
obviamente estos focos son los de la primera ecuación, si vas a poner los focos en la segunda ecuación debes cambiar la (C) en el eje y .
C²= a² - b²
Focos: F1 = (C,0) F2 = (-C,0)
si tienes el punto (C) tienes los focos
obviamente estos focos son los de la primera ecuación, si vas a poner los focos en la segunda ecuación debes cambiar la (C) en el eje y .
Focos: F1 = (0,C) F2 = (0,C)
también existe algo llamado excentricidad donde toda elipse satisface 0< e <1 donde jamas puede pasarse de 1 si se pasa es porque esta mal con esto podemos identificar si la elipse esta bien o mal la ecuación para la excentricidad es :
esto obviamente es mas y menos
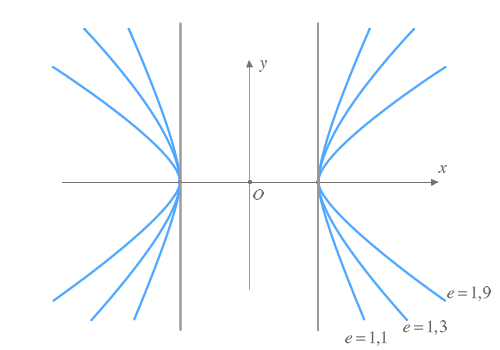
las asintotas son las lineas que van en la parte de la gráfica esta es la ecuación de las asintotas
las asintotas son las lineas rojas y lo azul son las "parábolas" y estas forman una hipérbola.
NO IMPORTA SI LA A ES MAYOR AQUÍ ES DEPENDIENDO LA DONDE ESTE LA ECUACIÓN
EJERCICIOS:
1.
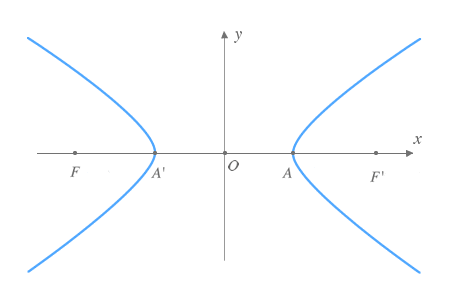
HIPÉRBOLA
a hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias a los puntos fijos llamados focos es constante en valor absoluto.
ecuación para la hipérbola:
Hipérbola de eje focal vertical centrada en el origen
y2a2−x2b2=1

Hipérbola de eje focal horizontal centrada en el origen
x2a2−y2b2=1

Excentricidad de la hipérbola
A partir de la semidistancia focal y el semieje real es posible obtener un valor numérico que nos indique como de "abierta" o "amplia" es una hipérbola. Dicho valor recibe el nombre de excentricidad.

ecuación de la excentricidad
e=ca
-vértices = ( a,0)
-focos = (C,0) C²= a² + b²esto obviamente es mas y menos
las asintotas son las lineas que van en la parte de la gráfica esta es la ecuación de las asintotas
las asintotas son las lineas rojas y lo azul son las "parábolas" y estas forman una hipérbola.
NO IMPORTA SI LA A ES MAYOR AQUÍ ES DEPENDIENDO LA DONDE ESTE LA ECUACIÓN
EJERCICIOS:
1.
DESARROLLO:
origen: 195mill +2150mill+68 mill r = 1075 mill diámetro = r + r
= 2413 / 2
= 1206,5 mill
a₁=(1205,5mill ,0) a₂=(-1205,5mill ,0) C²= a² - b
b₁=(0,546,6mill) b₂=(0,-546,6mill) -a²+c²= b²
F₁=(1075mill,0) F₂=(- 1075mill,0) 546,63mill=b
con la ecuación original remplazamos y esto es lo que nos da
DESARROLLO:
a₁=(40pulg,0) a₂=(-40pulg,0) C²= a² - b
b₁=(0,20pulg) b₂=(0,-20pulg) C²= √40² - 20²
F₁=(,20 √ 3 ,0) F₂=(-20 √ 3 ,0) C = √1200
C = 20 √ 3
remplazamos los datos obtenidos y despejamos (y)
√ y² = √ 899,60
DESARROLLO:
a. encontrar ecuación :
x²+y²= 16 x²/16 + y²/4 = 1 a = 4 b= 2
a₁=-4,0) a₂=(-4,0)
al tirar piedras al agua se forman ondas estas se chocan al chocarse sus interceptes forman puntos como coordenadas permitiendo que podamos identificar elipses y hipérbolas este es un claro ejemplo.
5.
5.
Hallar la ecuación de la hipérbola concentro en el origen, eje real paralelo al eje 0x, uno de cuyos vértices está en (−3, 0) y uno de sus focos en (5, 0). Determinar, además, las coordenadas de los extremos del eje imaginario y las ecuaciones de sus asíntotas.
Para los extremos del eje imaginario, es necesario avanzar desde el centro y de manera perpendicular al eje real, una distancia igual a b, tanto en un sentido como en otro, con lo cual se llega a los puntos B1(0, −4) y B2(0, 4).
Las ecuaciones de las asíntotas se obtienen a partir de las ecuaciones correspondientes al eje real horizontal, esto es:
Las ecuaciones de las asíntotas se obtienen a partir de las ecuaciones correspondientes al eje real horizontal, esto es:


















Comentarios
Publicar un comentario